Juego de formas

Estética en el espejo

La física describe la materia como un vacío que aparenta consistencia mediante puntos de carga energética. Hechos como este, y otros relativos a la teoría del conocimiento, han llevado a muchos pensadores a decir que la realidad no se puede captar por los sentidos, sino por la razón. Husserl habla de pasar del “objetivismo ingenuo” al “subjetivismo trascendental”.

Pero en el Teeto leemos como Sócrates enseña que, si bien es cierto que el saber no se puede fundamentar en lo que perciben los sentidos, tampoco puede hacerlo en los razonamientos o en la argumentación.

No se trata, por tanto, de ir de una realidad inconsistente a una realidad inmutable, sino de ir desde nuestras representaciones a la realidad. Para ello necesitamos una razón análoga, y la disciplina que la trata es la estética. La atención, por tanto, pasando primero por los contenidos mentales, habrá de llegar después a las formas estructuradoras.

Pero sus aspectos, -la medida, la proporción, el ritmo-, dan forma tanto a la dinámica del cosmos como a la humana. La Belleza, la conexión del espíritu con la armonía del mundo, nos recuerda esta estrecha ligazón.

Juego de Formas

Cuando Kepler se reconoce pitagórico convencido, Leibniz habla de las formas mentales, Kant de las formas de la sensibilidad, Euclides de la proporción divina o Platón de la geometría aurea, no desvarían irreflexivamente, pero nosotros sí vamos a cometer la ligereza de jugar con sus cuidadosas observaciones usando reglas escritas en el viento.

El punto sería el elemento de inicio de la partida, el uno que diferencia la existencia del vacío, pero en el triángulo encontramos la estructura básica de todas las demás construcciones geométricas y del pensamiento mismo. Todas las formas geométricas pueden dividirse en triángulos. Aristóteles plantea el silogismo lógico como una construcción tríadica, y Kant lo utiliza exhaustivamente cuando expone el concepto, lo parecido por defecto y lo parecido por exceso, para dejar claro su significado. Hegel le imprime dinámica con la tesis, antítesis y síntesis, y Zeising señala que es la forma fundamental del pensamiento.

Y, sin embargo, olvidan mencionar que la conexión entre los tres puntos que dibuja el triángulo es la intención. Pongamos que estamos tú, yo y, entre medias, un libro. ¿Lo olvidé y tú lo recogiste, te lo regalé deseando compartir contigo una historia, o te lo reclamaba? Sin una intención, sin una fuerza, no hay una relación posible.

La proporción aurea es la fórmula que utiliza la naturaleza para el crecimiento, y en ella el triángulo pasa a cuadrado manteniendo la misma área. Fi es el número que resulta de esta fórmula, y el pentágono, regular o estrellado, es su representación geométrica. Es por ello una forma frecuente en el mundo orgánico y muy rara en el inorgánico. Sin embargo, el cuadrado y el hexágono, -ambos operan con número enteros-, corresponden al mundo mineral.

La luz se descompone en tres colores básicos, y tres primarios, pero Newton dijo que eran siete, porque Pitágoras fijo en siete las notas musicales, y la llamada ley del siete o ley de octavas se extiende por toda la tradición antigua y clásica. Platón, el gran generador de mitos, -la caverna, el carro alado, la Atlántida, Prometeo, Sócrates, etc.-, recoge esta cosmogonía en su mito de Er, donde las tres parcas, representantes del tiempo, dan movimiento a la gran octava que es el modelo geocéntrico del universo.

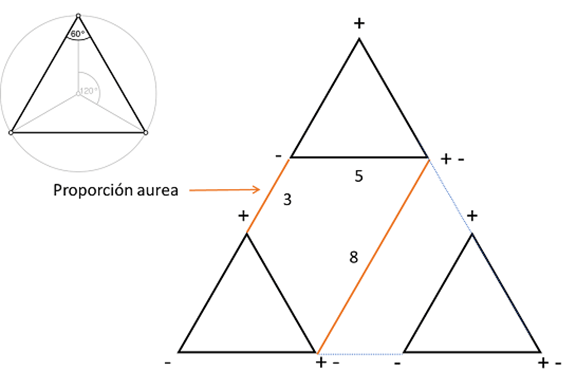
Pero si volvemos al triángulo de inicio, podemos encontrar el fundamento mismo de la proporción en uno equilátero que contenga a su vez una triada de triángulos, también de lados iguales.

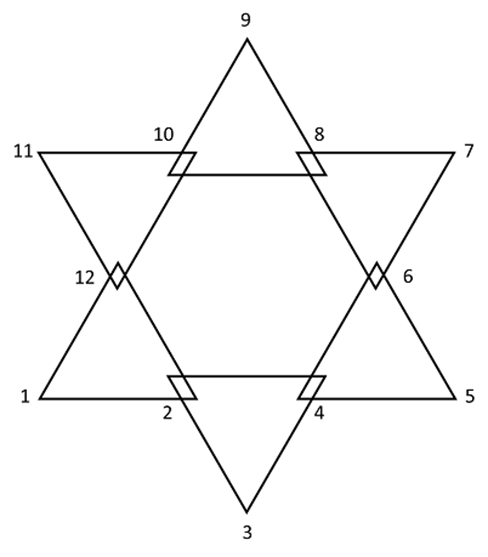
Gurdjieff, la tradición sufí, y otros, no sabemos si conscientemente, aplican la simetría geométrica, -la capacidad de un objeto de sufrir transformaciones de posición y movimiento, sin variar-, a los nueve puntos de a esta figura, componiendo así el eneagrama septenario, y de forma invertida el sextenario, representaciones formales de sus visiones de los procesos del comportamiento humano.

En dos dimensiones, la simetría pentagonal mantiene todos sus elementos en proporción aurea, pero en el mundo de tres dimensiones, el poliedro regular que mantiene esta proporción es el dodecaedro. Solapando los dos eneagramas obtenemos la estrella de seis puntas con doce ángulos, que desde la remota antigüedad dan lugar a todo tipo de relaciones entre el calendario, las divisiones celestes, los ciclos humanos y los cósmicos.

Sus doce lados se han pulido en la tradición hasta convertirlo en la esfera, representante del ciclo temporal, única forma sin lados ni partes, independiente de la reducción al triángulo, y que cierra el juego, dejándolo disponible para una nueva partida.